Intrinsically Ductile Refractory Alloy Development

Developing ductile refractory alloys has remained a challenge due to various design parameters put forth by different researchers to understand the intrinsic ductility of BCC alloys. Here I am focusing on the intrinsic ductility parameter (D) to develop concentrated refractory alloys.

The D is defined as,

$$ D = \frac{\gamma_s}{\gamma_{usfe}} $$

where, $\gamma_s$ is surface energy and $\gamma_{usfe}$ is unstable stacking fault energy. Under the framework of Density Functional Theory (DFT), the $\gamma_s$ is defined as,

$$ \gamma_s = \frac{E_{pristine}-E_{pristine+vac}}{2(Area\ of\ Surface)} $$

Here, the $E_{pristine}$ is the energy of the pristine supercell without any surface and $E_{pristine+vac}$ is the supercell having surface, i.e. the same pristine supercell is exposed to vacuum of suitable A (generally a vacuum of $\geq7A$ should suffice). The $\gamma_{usfe}$ is defines as,

$$ \gamma_{usfe} = \frac{E_{faulted}-E_{pristine}}{2(Area\ of\ Plane)} $$

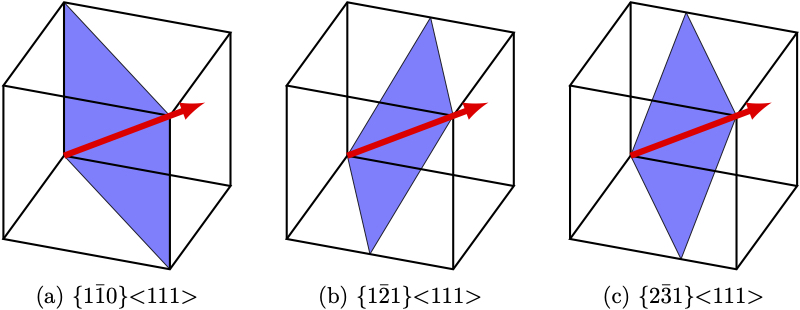
Here, the $E_{faulted}$ is the energy of supercell having a stacking fault and the $E_{pristine}$ is the energy of pristine supercell. The {110}<111> slip system of BCC metals/alloys has the lowest energy barrier for activation. Therefore, we have chosen the same slip system in present study.

First half of the supercell being sheared with respect to the bottom half. The code to generate the SQS is at generate_sqs repository.

There are total 10 shearings are occuring in the above video. For BCC crystal structure with burger’s vector $\bar{b}$,

$$ d = m \bar{b} $$

where $m\in[0.1,1.0]$. After every slip displacement d, the atoms are allowed to relax in all directions except the shearing direction. If the shearing direction is X, then the atoms are allowed to relax in Y and Z directions only.

Relaxation occuring in all directions except in the slip direction at the unstable stacking fault.

Accurate calculation of D requires an accurate estimate of $\gamma_s$ and $\gamma_{usfe}$. Therefore, in my Master’s Thesis I developed a methodology based on DFT framework to accurately calculate the $\gamma_s$ and $\gamma_{usfe}$ and quantify the errors associated with them.

The BCC crystal structure has 3 slip systems, $<111>\{110\}$, $<111>\{112\}$, and $<111>\{123\}$. Out of these 3 slip systems, the most acitve slip system in BCC crystals is $<111>\{110\}$. Rest 2 slip systems get activate at high temperature as the planes $\{112\}$ and $\{123\}$ are not as closed-packed as $\{110\}$. Majority of the deformation in BCC crystal occurs due the dislocation slip on $<111>\{110\}$ slip system. Therefore, we have focused on the $\gamma_{usfe}$ of the $<111>\{110\}$ and the $\gamma_{s}$ of $\{110\}$ plane. The intrinsic ductility parameter (D) has also been calculated for the same slip system.

Slip systems in BCC crystal.

Based on the above methodology our goal is to optimally reduce the number of alloys studied as we move from binaries to ternaries to higher-order alloy systems, as depicted in the figure below.

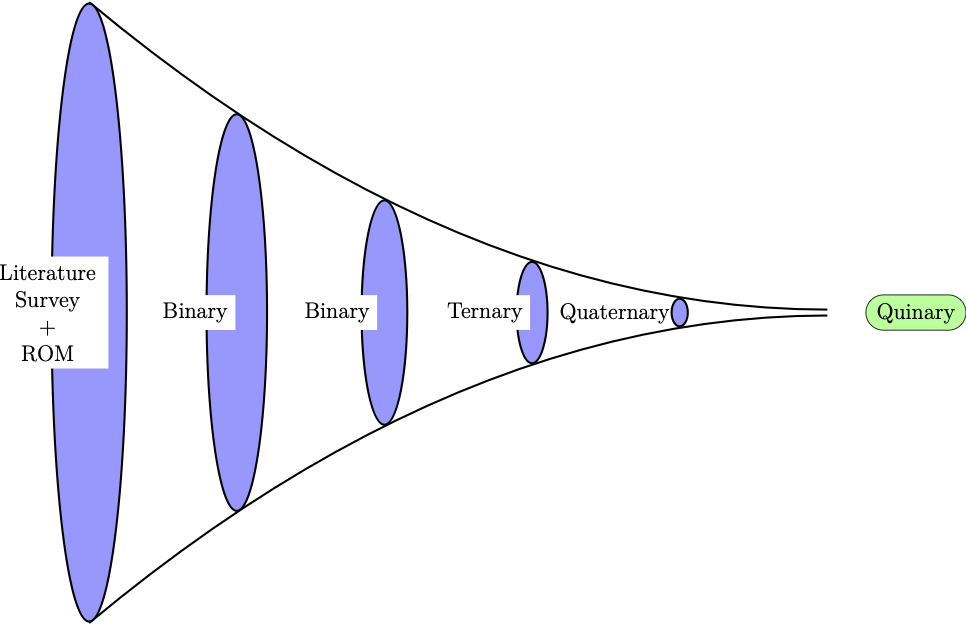
The alloy development funnel drastically reduces the number of systems to be studied.

The alloy development funnel ensures that the compositional explosion does not take place as we move from binaries to ternaries to higher-order alloy systems. What criteria to be selected to filter out alloy candidates is an integral part of my PhD dissertation. Every stage in the above funnel reduces the number of alloys to be studied based on specific property expectations criteria. This work has been published in the Journal of Applied Physics.

High Entropy Alloy presentation at CALPHAD-2020 Conference in Sweden.

Paradigm shift in alloy design where we combine the best of all constituent elements. I was one of the only 13 researchers worldwide in 2020 to be awarded the prestigious Larry Kaufman Scholarship. I presented this work at the CALPHAD conference in Sweden in May 2022.