Vibrational Entropy

This project is led by Rafshan-Ul-Atik who is a Master’s student in our research group.

The discussion below is taken from my publication:

The stability of an alloy (solid solution) is dictated by the Gibbs energy of its constituent phases as,

$$ \Delta G = \Delta H - T\Delta S $$

$$ \Delta G = \Delta E_f + {\Delta(PV)} - T\{\Delta S_{config} + \Delta S_{vib} + \Delta S_{mag} + \Delta S_{elec}\} $$

where \(\Delta E_f\) is the enthalpy of formation at 0K, \(\Delta(PV)\) is the pressure-volume term, \(\Delta S_{config}\) is the configurational entropy, \(\Delta S_{vib}\) is the vibrational entropy, \(\Delta S_{mag}\) is the magnetic entropy, and \(\Delta S_{elec}\) is the electronic entropy. The \(\Delta(PV)\) term can be ignored. Therefore the equation becomes,

$$ \Delta G = \Delta E_f - T\Delta S_{config} - T\{\Delta S_{vib} + \Delta S_{mag} + \Delta S_{elec}\} $$

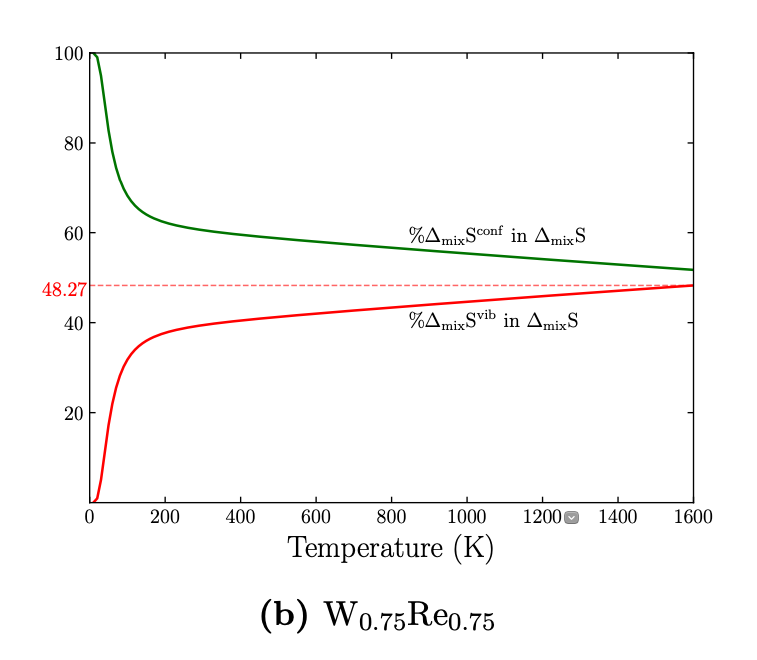
Our focus in present work is to understand how much \(\Delta S_{vib}\) is contributing to the overall \(\Delta S\). We found that contrary to the long held notion that the \(\Delta S_{config}\) is the primary reason for calling “High Entropy Alloy” as “High Entropy”, it is the \(\Delta S_{vib}\) which is contributing majorly to the overall entropy in concetrated alloys. We observed this after studying the absolute entropy \(S\) and the difference of entropy \(\Delta S\) of alloy with its constituent elements. This work has been published and has been submitted.